If you are doing vector search with a vector library that supports SVE, you should use a Graviton 3 machine. It is cheaper, and it will also deliver more raw performance.
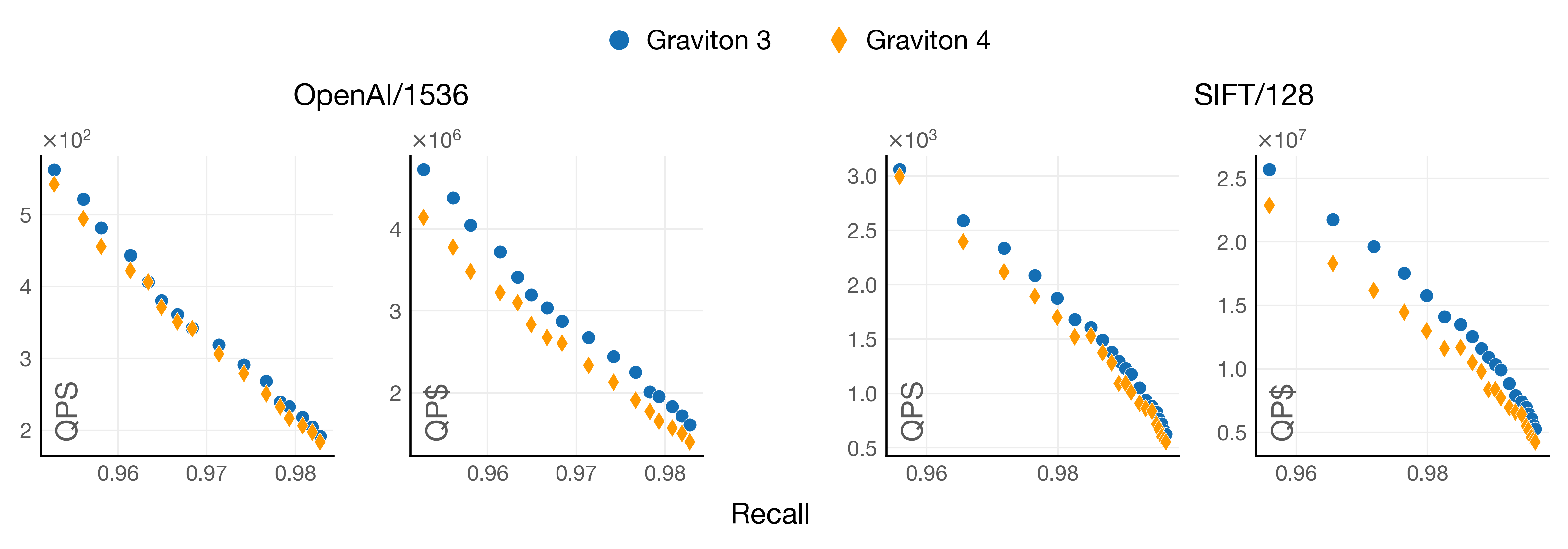
A few months ago, we started working on a vertical layout for vector similarity search (PDX). As part of the benchmarks that we were running on different microarchitectures and vector systems like FAISS, Milvus, and Usearch, there was an observation that puzzled us: Graviton3 performed better than Graviton4 in almost all vector search scenarios, not only in queries per dollar (QP$) but also in queries per second (QPS). This was the case across vector libraries and even in our implementations of vector search algorithms. Here is one example of the QPS and QP$ of both microarchitectures on queries to an IVF index:
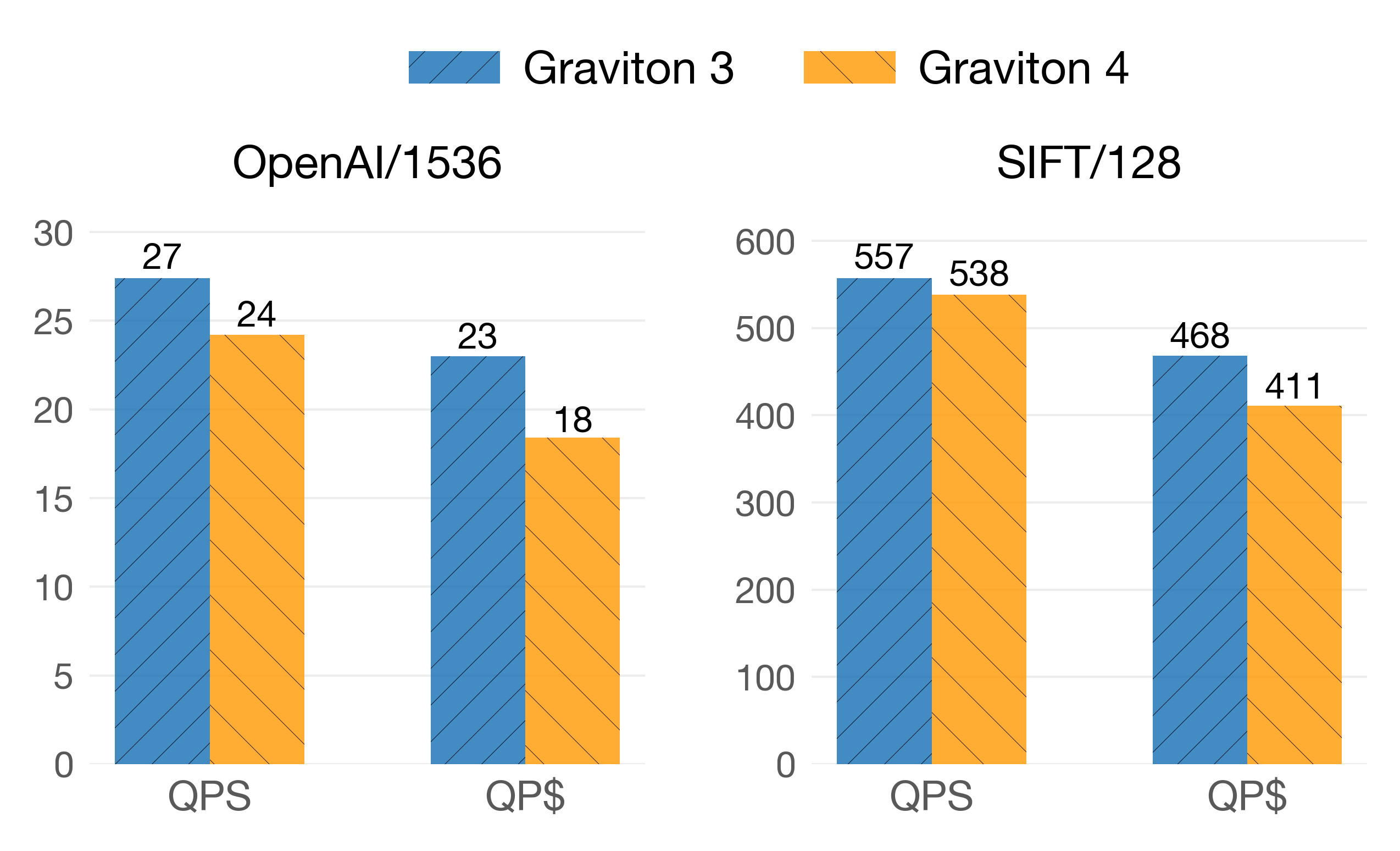
Recall@10: 0.99 on IVF indexes (float32) built with FAISS+SVE. QP$ are in the order of 10^4.
In the OpenAI/1536 dataset with 1M vectors, Graviton3 delivers 25% more queries per dollar than Graviton4!
Let’s be clear: Graviton4 is a better machine than Graviton3. It has a higher clock frequency, a 2x bigger L2 cache, a slightly bigger L3, less memory-access latency, and a much more capable CPU (upgrading from Neoverse v1 to Neoverse v2). This is shown not only by AWS but also by innumerable benchmarks. I can refer to the benchmarks done by Daniel Lemire, Phoronix, and Chips and Cheese. But then, why would Graviton3 be better than Graviton4 on Vector Similarity Search?
The main culprit is that Graviton4 has a SVE SIMD register size of 128 bits —half of the 256-bit registers of Graviton3.
In the rest of this blog post, we will dive deep into why this difference is particularly detrimental to the performance of vector similarity search and why this hasn’t been picked up by other benchmarks. But before discussing about the Gravitons, let’s refresh our knowledge of SIMD.
SIMD in Vector Similarity Search
Distance calculations in vector similarity search can be optimized using Single-Instruction-Multiple-Data (SIMD) instructions available in the CPU. These special instructions can process multiple values in parallel with a single CPU instruction.
In x86_64 architectures, SIMD instructions are called Advanced Vector Extensions (AVX). The number of values AVX can process at a time depends on the SIMD register width supported by the CPU. Modern CPU microarchitectures, like Zen4 and Intel Sapphire Rapids, have 512-bit SIMD registers (AVX512), which can process 16 float32 values with one CPU instruction.
Let’s look at the following C++ code (taken from the SimSIMD codebase) that uses AVX512 SIMD to calculate the Euclidean distance (L2) between two vectors:
| |
The critical part is the l2sq_f32_loop that loops through the vector dimensions. In each iteration, _mm512_loadu_ps loads 16 packed single-precision values (32 bits each) into the SIMD register. We do this twice, once for vector a and another for vector b. Then, we do the L2 calculation by doing a subtraction (_mm512_sub_ps) and a fused multiply-add (_mm512_fmadd_ps) that accumulates the distances into a result register (d2_vec). We keep repeating the loop until we have inspected all the vector dimensions (when n == 0). Finally, we have to sum all the values in the SIMD register to get our total distance (reduce_f32x16). We will obviate the explanation of this last step.
On the other hand, ARM architectures also provide SIMD instructions through NEON and SVE. NEON was introduced first, supporting SIMD over 128-bit registers (fitting 4 float32 values at a time). SVE was introduced later. Unlike AVX and NEON, SVE supports variable-size SIMD registers on its intrinsics through VLA (Variable Length Agnostic) programming. The latter alleviates technical debt as distance kernels no longer need hardware-dependent loop lengths.
Let’s take a look now at a code with SVE intrinsics (also taken from SimSIMD):
| |
svld1_f32 is the SIMD intrinsic that loads the single-precision vector into the SIMD register. svsub_f32_x and svmla_f32_x do the subtraction and fused multiply-add, resp. The main difference between SVE and AVX512 is that each loop iteration length is not controlled with a constant but with another intrinsic (svcntw()) that resolves to the register width of the underlying CPU. Recall that in the AVX512 code, we do n-=16 to advance through the loop. SVE has additional intricacies. For example, every intrinsic call must be predicated/masked. But we will not dive deep into SVE programming.
Back to the Gravitons: From 256-bit to 128-bit SVE registers
Both Gravitons support NEON and SVE SIMD. In terms of NEON, both microarchitectures have 128-bit SIMD registers. However, in terms of SVE, Graviton4 has 128-bit registers, while Graviton3 has 256-bit registers.
A smaller SIMD register does not mean slower performance. Yes, every instruction call will process fewer values, but the performance also depends on the execution throughput and latencies of the used instructions. The execution throughput is defined on ARM guides as “the maximum number of instructions per CPU cycle an instruction can achieve.” The latter depends on the CPU design and the ports in which CPU instructions are dispatched. On the other hand, latency is defined as “the delay (in clock cycles) that the instruction generates in a dependency chain.”
Let’s compare both microarchitectures execution throughput and latencies on the relevant instructions for our L2 distance kernel: FMADD and LOAD.
Execution Throughput
The first number in each cell is the execution throughput. To translate this to effective throughput of data, we multiply it by the size of the register that executes that instruction.
| Microarchitecture | NEON FMADD | SVE FMADD | NEON LOAD | SVE LOAD |
|---|---|---|---|---|
| Graviton 3 (Neoverse v1) | 4 x 128 = 512 | 2 x 256 = 512 | 3 x 128 = 384 | 2 x 256 = 512 |
| Graviton 4 (Neoverse v2) | 4 x 128 = 512 | 4 x 128 = 512 | 3 x 128 = 384 | 3 x 128 = 384 |
*These numbers are taken from the official microarchitecture guides of Neoverse v1 and Neoverse v2
We see that Graviton4 maintains the execution throughput of floating-point arithmetic despite the smaller register width. From these numbers, only one stands out: the SVE LOAD. Graviton3 can load 33% more data than Graviton4 in one CPU cycle, which is more than the upgrade in clock frequency from Graviton3 to Graviton4 (around 8%). This gives an advantage to Graviton3 if the data is cache resident. In fact, this is reflected in our read memory bandwidth benchmarks that show that when data is L1-resident, the read bandwidth using SVE intrinsics is 26% higher in Graviton3.
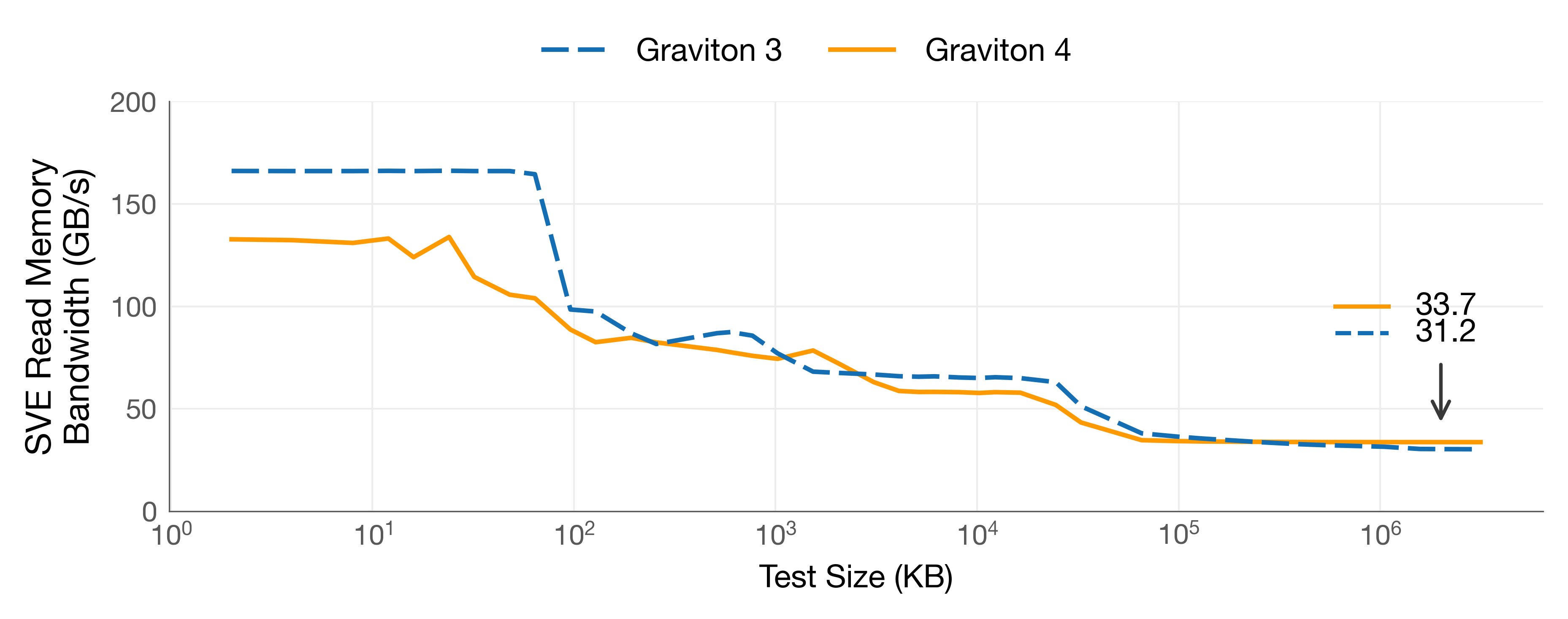
SVE Read Memory Bandwidth on Graviton3 (r7g.metal) and Graviton4 (r8g.metal-24xl)
However, in vector search, we are usually on the case in which data is in L3/DRAM (in IVF indexes or full scans) or, at best, in L2 (e.g., in the top layer of HNSW indexes). Here, the difference in read bandwidth is small.
Latencies
| Microarchitecture | NEON FMADD | SVE FMADD | NEON LOAD | SVE LOAD |
|---|---|---|---|---|
| Graviton 3 (Neoverse v1) | 4 | 4 | 4 | 6 |
| Graviton 4 (Neoverse v2) | 4 | 4 | 4 | 6 |
*These numbers are taken from the official microarchitecture guides of Neoverse v1 and Neoverse v2
The latencies are the same in both CPUs. However, the total latency cost to load the same amount of data is higher in Graviton4 due to the smaller register width. For example, the latency cost of calling FMADD in Graviton4 to process 128 bits (4 float32 values) is 4 cycles. However, in Graviton3, we spend the same 4 cycles to process 256 bits (8 float32 values).
Also, recall that in our AVX and SVE code of the L2 distance kernel, each iteration of the loop depends on the previous one since all the FMADDs are accumulating distances on the same SIMD register. This creates a dependency chain, making it harder for the CPU to leverage features such as out-of-order execution. Therefore, the SIMD register width becomes more critical in similarity calculations, as instructions may not be able to be executed in parallel up to their maximum throughput.
Of course, it is hard to precisely determine the impact of these extra cycles and less effective throughput on the bigger picture of a vector similarity search query. Each CPU microarchitecture is wildly different and implements different mechanisms to maintain performance despite having a smaller register width. Therefore, let’s run some benchmarks!
Benchmarks: Graviton 3 vs Graviton 4
We compared the queries per second (QPS) and queries per dollar (QP$) given by Graviton3 (r7g.2xlarge, $0.4284/h in us-east-1) and Graviton4 (r8g.2xlarge, $0.4713/h) on a variety of vector search scenarios. The machines have Ubuntu 24 with GCC 13 and LLVM 18.
We used 2 datasets contrasting in their dimensionality:
- OpenAI (D=1536, N=1M)
- SIFT (D=128, N=1M)
For these single-threaded benchmarks, we used FAISS (compiled with SVE) and USearch.
IVF Indexes in FAISS
Graviton3 performs better at all recall levels and even more so in the dataset of higher dimensionality. Things look worse for Graviton4 when we consider its price, as Graviton3 is a cheaper machine (around 10% cheaper).
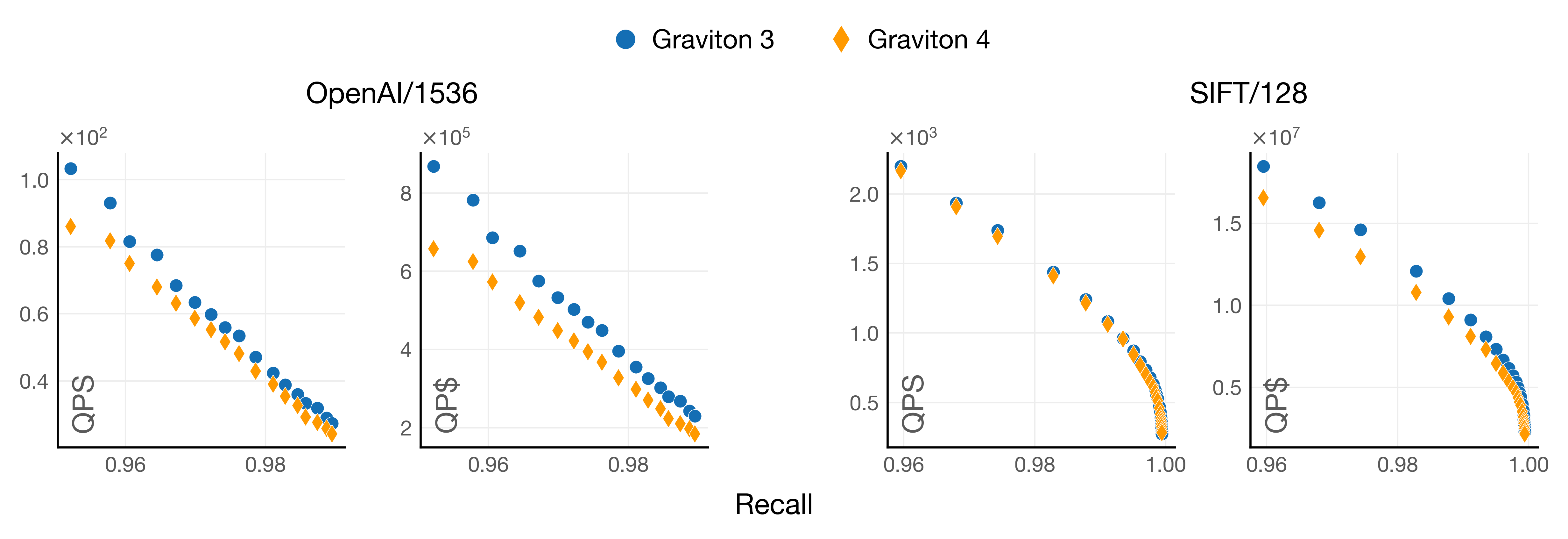
Notice how the gap closes on the dataset with a lower dimensionality. However, it is nowhere near the 30% performance improvement AWS promises when jumping from Graviton3 to Graviton4.
HNSW Indexes in USearch
On float32, again, Graviton3 performs better at all recall levels. Graviton3 delivers 5% more QPS and 15% more QP$ in the OpenAI dataset at the highest recall level. And 13% and 25% more QPS and QPS, resp., in the SIFT/128 dataset.
The story is the same for quantized vectors. Here, we show only the performance at the highest possible recall level:
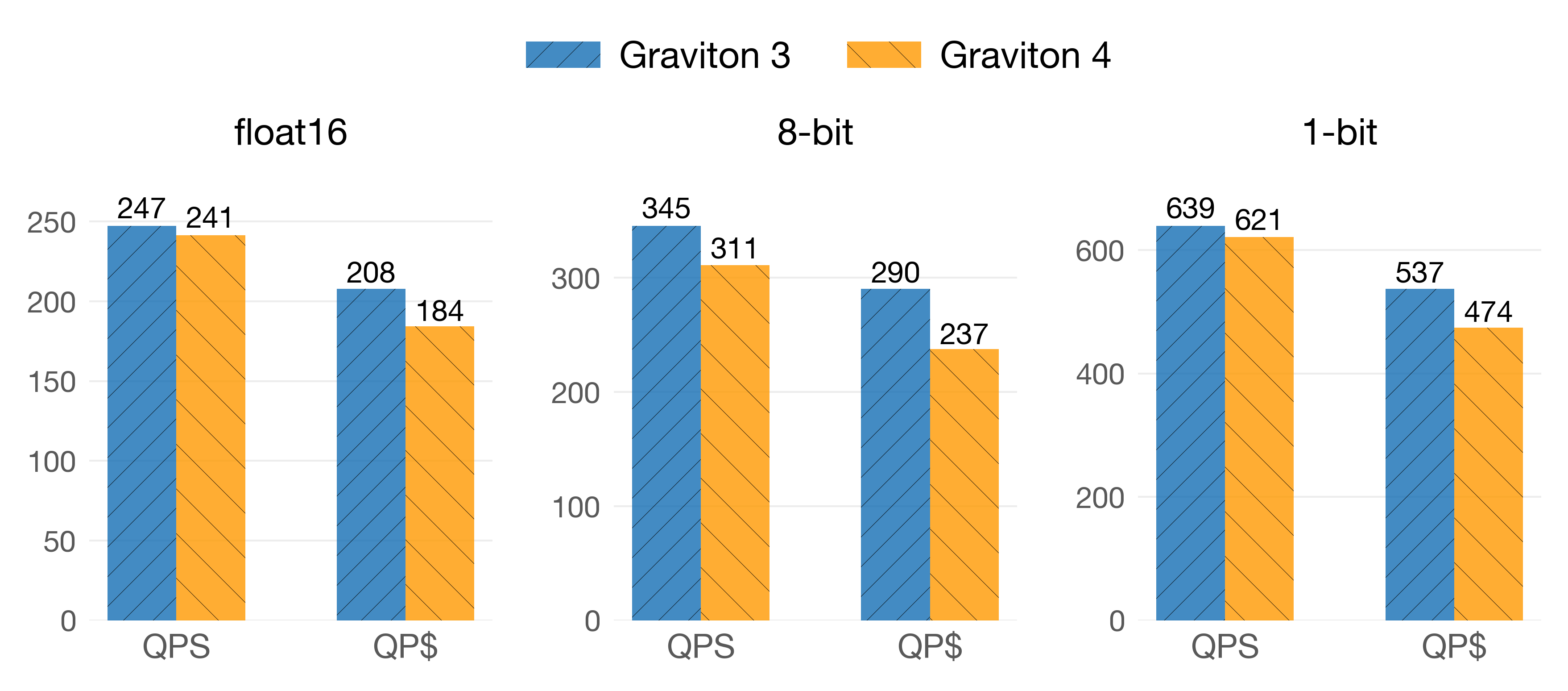
On the OpenAI/1536 dataset
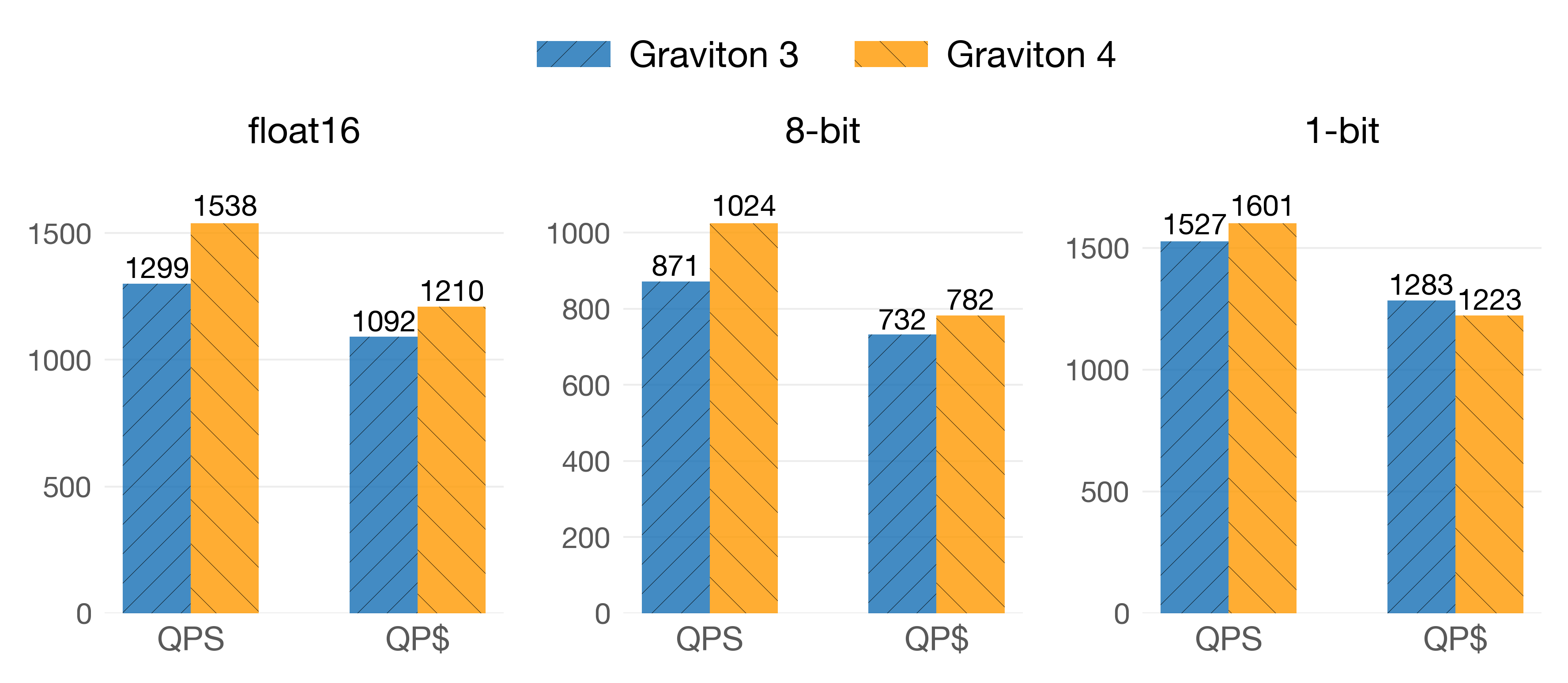
On the SIFT/128 dataset
In the dataset of smaller dimensionality (SIFT/128), G4 takes the upper hand on QPS, but G3 remains competitive on QP$. Here, the bigger L2 of G4 could be kicking in due to the entry nodes of the HNSW index being cached more efficiently. Also, smaller vectors imply fewer calls to SIMD instructions, which benefits G4.
Note 1: USearch switches to NEON for 1-bit vectors if the vectors are of 128 dimensions, which is the case here.
Note 2: We did not benchmark quantized vectors in FAISS because FAISS does asymmetric distance calculations. This in itself would not be a problem, but for ARM, FAISS does not use SIMD instructions to go from the 8-bit, 6-bit, 4-bit domain to the float32 domain. This leads to poor performance in both architectures (>6x slower than Zen4).
Raw Distance Calculations (1-to-many)
We ran a standalone benchmark of L2 distance calculations to eliminate possible artifacts and overhead introduced by vector systems. Here, we used randomly generated float32 collections of different sizes and dimensionalities. The collections range from being small enough to fit in L1 and large enough to spill to DRAM. Our code is as simple as it can get: Put the vectors in memory and do 1-to-many distance calculations with the L2 kernels taken from SimSIMD. Here, we do not do a KNN search; we only do pure distance calculations. We repeat this experiment thousands of times to warm up the caches.
NEON vs NEON
When using NEON kernels, Graviton4 is, on average, 10% faster than Graviton3 across all settings. This improvement is on par with the increase in clock frequency between both microarchitectures.
SVE vs SVE
When switching from NEON to SVE, Graviton3 saw a 37% performance improvement over its NEON counterpart. Ash Vardanian also reported similar findings. However, Graviton4 doesn’t find any benefits when using SVE (in fact, compiling FAISS to SVE or not yields the same performance). Actually, SVE is slightly slower than NEON in G4. These could be fluctuations/noise of the benchmarks or the overhead of masked operations in SVE.
When comparing G3 SVE vs G4 SVE, these are the results across scenarios:
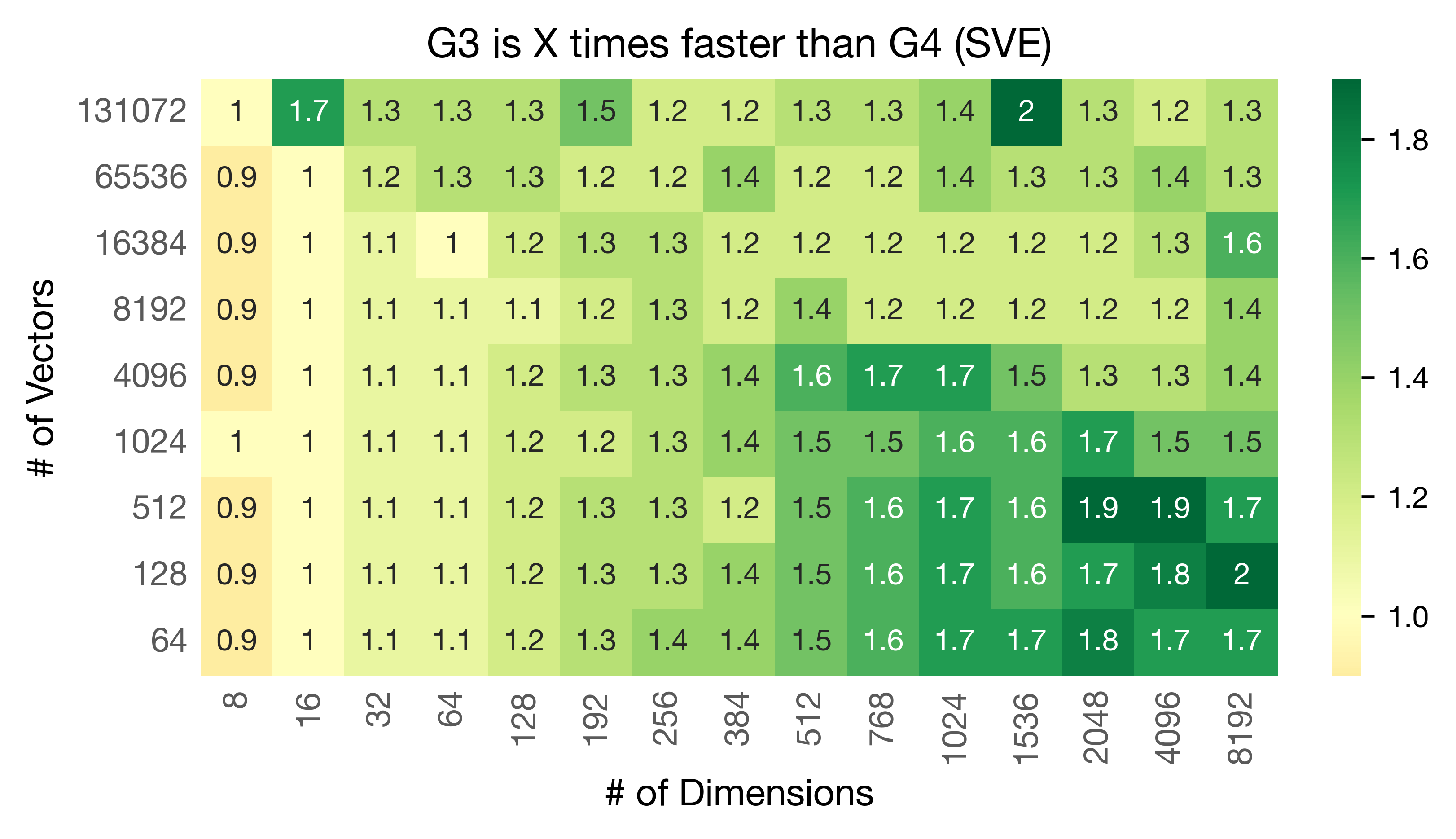
Graviton3 is, on average, 31% faster than Graviton4.
You can check these fully disaggregated benchmarks for each collection size and dimensionality on this spreadsheet. We would like to bring forward a few things regarding these benchmarks: (i) The wider the vectors, the bigger the gap between G3 and G4. (ii) If the vectors fit in the cache, Graviton3 can be almost 2x faster than Graviton4. (iii) Only at a dimensionality of 8, the tables turn, and Graviton3 is slightly slower than Graviton4.
The benchmarks are clear: if you are doing vector search with a vector library that supports SVE, you should use Graviton 3. It is cheaper, and it will also deliver more raw performance in the majority of scenarios.
Why did Graviton4 regress the SVE register width?
While we do not have a proper answer to this question, we can speculate.
Currently, most code for ARM is written in NEON, where Graviton4 is better than Graviton3. A possibility is that AWS went for a CPU that performed better in existing workloads and benchmarks, which usually use code written in NEON. In fact, Daniel Lemire and Chips and Cheese benchmarks on Graviton4 vs Graviton3 used NEON code. In other words, SVE is not yet widely used.
Another possible reason is that SIMD instructions can be fully pipelined in many workloads. However, similarity calculations are different because there is a dependency chain between multiple calls to SIMD instructions. The latter benefits wider registers, especially on vectors of high dimensionalities. While we haven’t done benchmarks on SVE for other types of workloads, our intuition is that if the workload can be fully pipelined, it would be faster in Graviton4.
Closing Remarks
I have found myself inside a (nice) rabbit hole of CPU microarchitecture design and performance. We have actually done the same experiments presented in this blog post for 5 microarchitectures (Intel SPR, Graviton3, Graviton4, Zen3, and Zen4). One of our most interesting findings is that carefully choosing the microarchitecture for your vector search use case can give you up to 3x more queries per second and queries per dollar. This is the case, for instance, with Zen4 in IVF indexes compared to Intel Sapphire Rapids (despite the latter being a CPU with better specs). I am writing a blog post about that, so keep tuned!
Regarding the Gravitons, it is nonetheless a weird decision to halve the SIMD register size in the generational jump from Graviton3 to Graviton4. Perhaps in terms of the engineering design of the core, it is hard to keep supporting NEON registers of 128 bits AND SVE registers of double the size.
Not so far ago, Daniel Lemire commented that “AMD is mopping the floor with ARM in terms of SIMD.”
To my knowledge, the best NEON offers is 4 x 128-bit, so four 128-bit instructions per cycle.
— Daniel Lemire (@lemire) February 11, 2025
AMD is at 4 x 512-bit... and that's AVX-512, so much more powerful than NEON.
So on SIMD... AMD is just mopping the floor with ARM.
ARM has SVE/SVE2 but that does not seem to be going… pic.twitter.com/9AvOQW8lzl
It is no rocket science: a smaller register will impact the performance of some workloads, even if the execution throughput is kept the same. Of course, when comparing different microarchitectures, more things come into play, such as memory access latency, read memory bandwidth, and the data-access patterns of the workload. Ultimately, your decision to use a microarchitecture should be based on data-driven benchmarks with your own use case. As you may have noticed, the performance depends on various factors, such as the search algorithm and the size of the vectors. Perhaps an interesting follow-up post would be to test both architectures by doing vector search under a multi-threaded setting.
For now, it seems that aside from the portability benefits, there is currently not much payoff in migrating NEON code to SVE, especially if the cores used by AWS will keep the SVE register size on par with NEON. The only exception would be when one needs to use an intrinsic that is only available in SVE.
Kudos to Ash for giving input on these findings and for putting them forward to the ARM team. We are still awaiting their input.